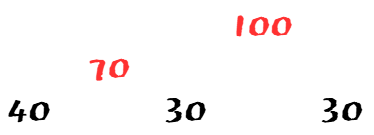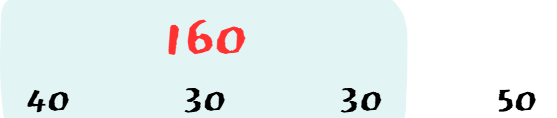[알고리즘] 백준 - 파일 합치기(11066번) [JAVA]

파일 합치기

2차원 배열을 이용한 누적합을 구하는 것처럼 상당히 까다로웠던 문제였다. 모르면 맞아야되는 문제 중 하나라고 생각한다. 점화식을 유도했어야 했는데 쉽사리 유도해내지도 못했다. 때문에 인터넷 + GPT의 도움을 받았다.

---

의식의 흐름

1차원 배열만으로는 부분 부분의 합을 고려할수가 없다.

“각 원소의 합들을 구한 후에 2차원 배열을 통해 그 값들을 저장한 후 다음에 있을 처리에 써먹는다.” 가 이 문제의 포인트다.

말보다는 그림을 통해 이해하는 편이 편할것이다.

그림을 추가한 풀이

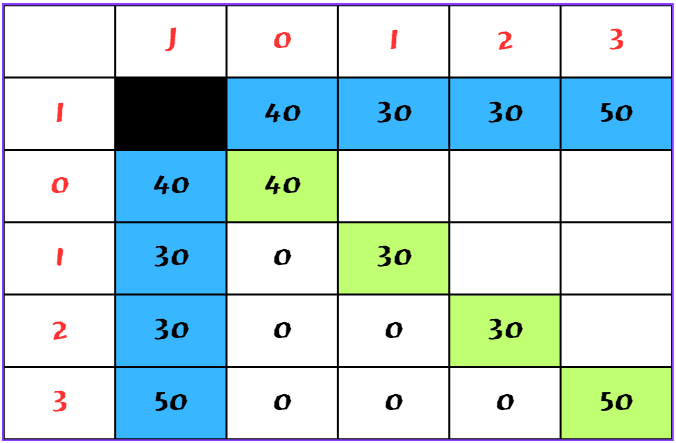
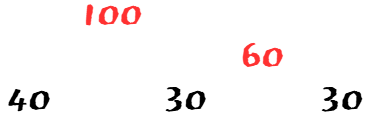
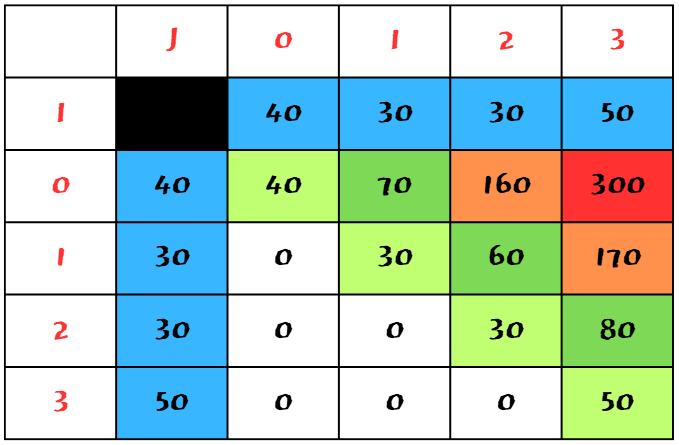
위 표의 I는 시작 index를 말하며, j는 끝 index를 의미한다. i부터 j 번째까지의 합을 적을 표다.

당연하게도 0부터 0까지의 합은 40이고 1부터 1은 30이다. 그것부터 채워넣었다.

0 ~ 1, 1 ~ 2, 3 ~ 4까지의 합을 각 칸에 넣는다.

여기까지는 문제가 없다. 어차피 경우의 수가 1밖에 없기 때문에 반드시 최소값이다.

여기서부터가 문제다. 어떻게 점화식을 추출할 수 있을까?

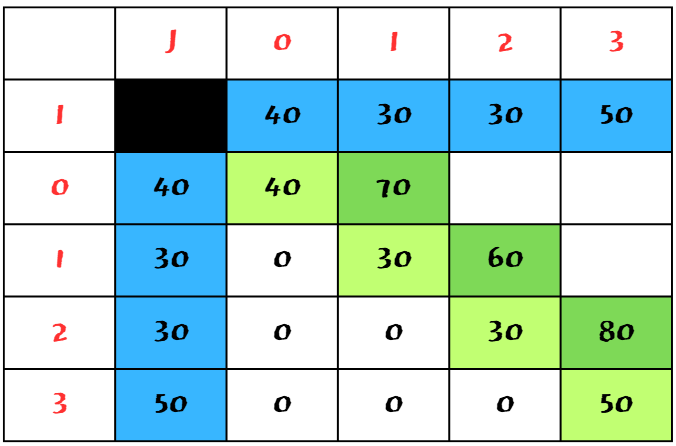
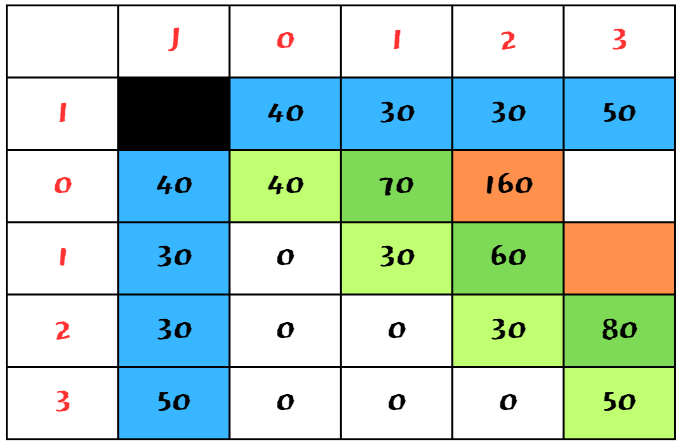
0 ~ 2 까지의 경우의 수는 다음과 같다.

0 ~ 1 후 2 더하기 = 70 + 100 = 170

or

1 ~ 2 후 0 더하기 = 60 + 100 = 170

170과 160 중 160이 더 작으니, 160을 취하고 표를 채워넣었다.

여기서 우리가 발견해야할 insight는 100이라는 숫자다.

공통적으로 마지막에 100이라는 숫자를 더해준다.

이는 곧, 연산의 마지막에 40 + 30 + 30을 (모든 원소를 한번씩 더함) 한 값이된다.

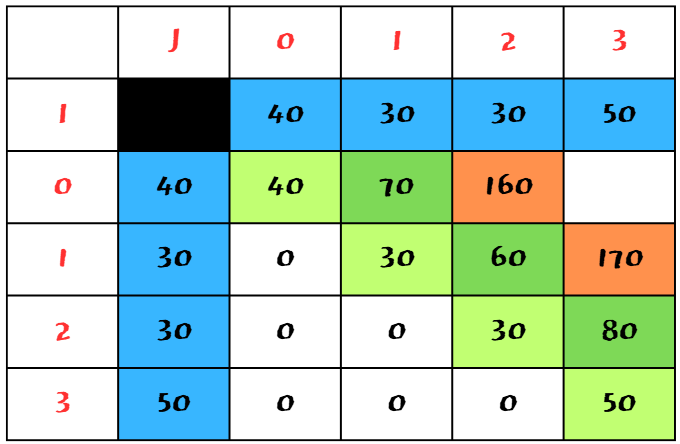
우연일지도 모르니 1 ~ 3의 과정도 해보자.

1 ~ 2 후 3 더히기 = 60 + 110 = 170

2 ~ 3 후 1 더하기 = 80 + 110 = 190

170과 190 중 170이 더 작으니, 170을 취하고 표를 채워넣었다.

마찬가지로 마지막에 동일한 110 이라는 숫자가 더해졌다.

이를 통해 생각해보면, (i, j)를 구하기 위해 부분 합 + (i ~ j에 해당하는 모든 원소들의 합)이 되는 것임을 다시한번 알 수 있다.

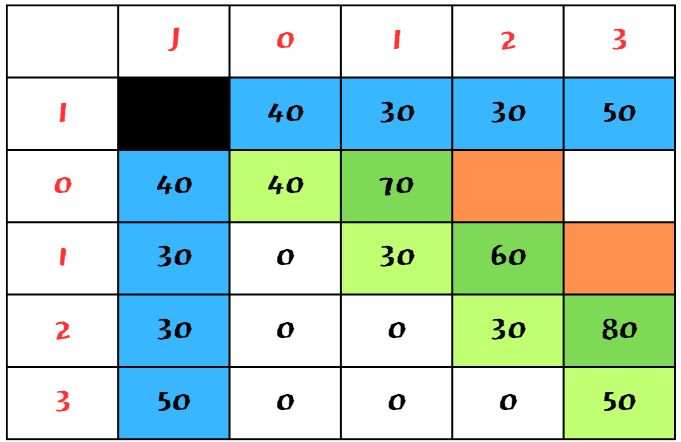
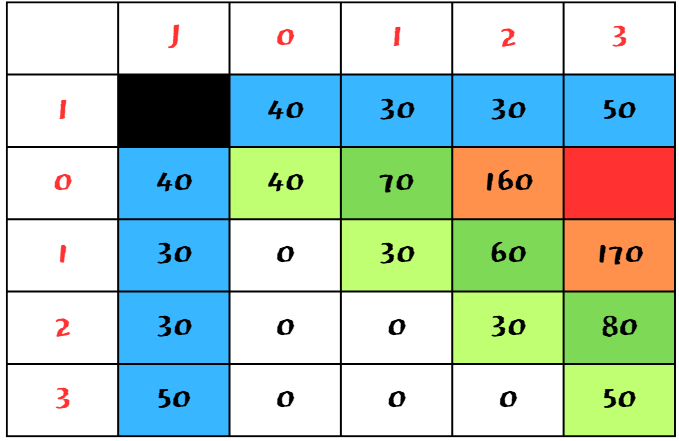
마지막으로 빨간 부분을 구하여야 한다.

0 ~ 2 최소값은 160

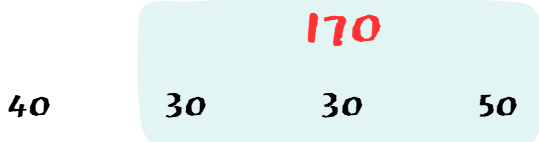
1 ~ 3 최소값은 170 이다.

각각 다음 그림과 같다.

그 다음 마지막 남은 원소가 아닌, 0 부터 3까지 더한 값(150)을 더해주면 (왜 이렇게 더하는지는 윗 부분을 다시 보고오면 알것이다.)

160 + 150 = 310

170 + 150 = 320

그럼 310이 답인가?

간과하고 있는건, (0 ~ 1) + (2 ~ 3)의 조합이다.

아래 그림을 보자.

70 + 80 + 150(모든 원소의 합) = 300

즉, 300이 답이된다.

0 ~ 3 의 값을 찾기 위해서는

(0 ~ 2) + 모든 원소의 합 = 160 + 150 = 310

(1 ~ 3) + 모든 원소의 합 = 170 + 150 = 320

까지는 3개 원소씩 묶었고, 2개씩 묶는 조합도 있다.

(0 ~ 1) + (2 ~ 3) + 모든 원소의 합 = 70 + 80 + 150 = 300

모아 보면

(0 ~ 2) + (3)

(0 ~ 1) + (2 ~ 3)

(1) + (1 ~ 3)

최종적으로 i 부터 j까지의 합을 찾기 위한 방법은

(i <= m < j) 의 범위 안에서
(i ~ (m)) + ((m + 1) ~ j) 이 나오고
위에서 나오는 값들 중에서 가장 작은 값을 취하고
마지막으로 모든 원소의 합을 더하면 된다.

점화식은 아래와 같다.

dp[i][j] = sum(j) - sum(i) + {
        for(m = k; m < j; m++ ){
            (i ~ (m)) + ((m + 1) ~ j) 의 합
        }
        마지막으로 가장 작은 값 추출 후 반환
    }

sum(j) - sum(i)의 이유는 j까지의 합에서 i까지의 합을 빼줘야만, 해당하는 특정 부분의 원소들의 합을 구할수 있다.

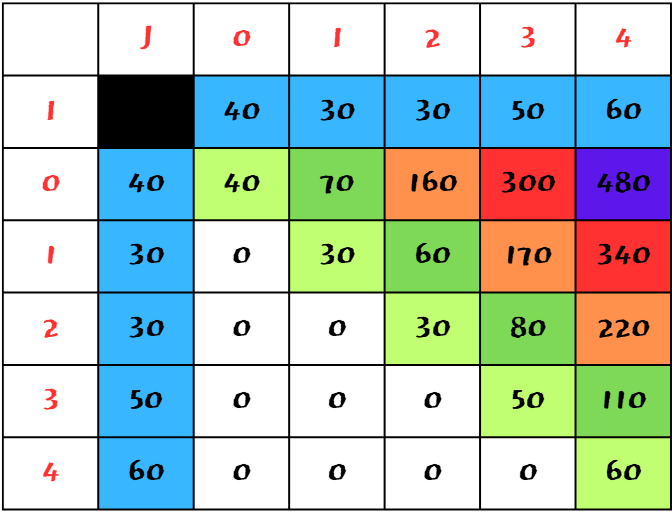
이해를 돕기위해 원소를 하나 더 추가해서 돌려보겠다.

(0 ~ 4)를 구하기 위해서는 다음과 같은 조합이 나온다.

(0) + (1~4), (0 ~ 1) + (2 ~ 4), (0 ~ 2) + (3 ~ 4), (0 ~ 3) + (4)

각각

(0) + (1 ~ 4): 40 + 340 = 380

(0 ~ 1) + (2 ~ 4) : 70 + 220 = 290

(0 ~ 2) + (3 ~ 4) : 160 + 110 = 270

(0 ~ 3) + (4) : 300 + 60 = 360

이후 270을 취하고 각 원소의 합까지 더하면

270 + 210 (인덱스 0부터 4까지 각 원소의 합) = 480

답은 480.

---

마지막으로 코드 부분이다.

코드 (JAVA)

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;

public class Main {

  public static void main(String[] args) throws IOException {
    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    StringBuilder sb = new StringBuilder();

    int T = Integer.parseInt(br.readLine());
    for (int i = 1; i <= T; i++) {
      int K = Integer.parseInt(br.readLine());

      int[] arr = Arrays.stream(br.readLine().split(" "))
          .mapToInt(Integer::parseInt).toArray();

      if (arr.length == 1) {
        sb.append(arr[0]);
        System.out.println(sb);
        return;
      } else if (arr.length == 2) {
        sb.append(arr[0] + arr[1]);
        System.out.println(sb);
        return;
      }

      int[][] dp = new int[K][K];

      int[] sum = new int[K];

      sum[0] = arr[0];

      for (int j = 1; j < K; j++) {
        sum[j] = sum[j - 1] + arr[j];
      }

      for (int j = 0; j < K - 1; j++) {
        dp[j][j + 1] = arr[j] + arr[j + 1];
      }

      boolean flag = true;
      int plus = 2;

      while (flag) {
        int x = 0;

        for (int y = x + plus; y < K; y++) {

          int min = Integer.MAX_VALUE;

          for (int k = x; k < y; k++) {
            min = Math.min(min, dp[x][k] + dp[k + 1][y]);
          }

          dp[x][y] = min + (sum[y] - (x == 0 ? 0 : sum[x - 1]));

          if (y == K - 1) {
            plus++;
            if (x == 0) {
              flag = false;
            }
          }

          x++;
        }
      }

      sb.append(dp[0][K - 1]).append("\n");
    }

    System.out.print(sb);
  }
}

소감

이해하고 나니까 속은 시원한데, 이걸 과연 내가 혼자서 유도까지 할 수 있을까? 라고 하면 아직은 무리일듯 싶다.

힘든 하루였다.